의사결정나무(Decision Tree)는 데이터에 내재되어 있는 패턴을 변수의 조합으로 나타내는 예측 / 분류 모델을 나무의 형태로 만든 것이다. 과거에 수집된 자료를 분석하여 이들 사이에 존재하는 패턴을 나타내는 모델을 나타낸다.
질문을 던져서 맞고 틀리는 것에 따라 우리가 생각하고 있는 대상을 좁혀나가게 된다. 예전에 '스무고개' 게임과 비슷한 개념이다. 사람이 스무번의 질문을 던지면서 하나의 정답을 맞춰나가는 과정이 이와 매우 유사하다.
데이터가 입력되었을 때 알고리즘에 의해 데이터를 2개 혹은 그 이상의 부분집합으로 분할하게 된다. 분류-의사결정나무의 분할는 비슷한 범주를 갖고 있는 관측치끼리 모으는 것이고 예측-의사결정나무의 분할은 비슷한 수치를 갖고 있는 관측치끼리의 모음이다. 이러한 과정을 지속적으로 반복하면서 최종적으로 만족할 만한 구조가 나오면 그 형태의 트리가 의사결정나무 모델이 된다. 자세한건 좀 더 살펴보자.
의사결정나무의 구조

의사결정나무의 구조는 다음 과 같다
- Root Node : 전체 학습 데이터
- Internal Node : 중간 노드, Leaf 노드가 아닌 노드
- Leaf Node : 끝 노드, 자식 노드가 없는 가장 하위의 노드
- Level : 루트 노드를 기준으로 특정 노드까지의 경로 길이
- Depth : 의사결정나무의 깊이, 트리의 최대 레벨
- Branch : 노드와 노드를 잇는 선
- Parent Node : 자식 노드의 상위 노드
- Child Node : 하나의 노드로부터 분리된 2개 이상의 노드
- Sibling Node : 같은 부모를 가진 노드, Depth가 같다.
예측 의사결정나무 (Regression Tree)
예측나무의 기본적인 아이디어는 아래와 같다. 예측나무는 종속변수 Y를 예측하는 모델이다. 아래 그림을 보자.
왼쪽 그림을 보면 독립변수 X1, X2에 대한 값이 존재하고 원은 관측치이다. 관측치마다 X1, X2값이 있고, Y값이 있다. 예측모델에선 X1, X2, Y 모두 수치형 변수이다. 나누는 법칙은 생각하지 않고 일단 오른쪽 그림처럼 총 5개의 부분집합으로 나눴다고 가정하자.
오른쪽 그림이 결국 예측나무 모델이 된다. 모델을 생성했다면 새로운 데이터에 대한 Y값을 예측할 수 있는지 테스트가 필요하다.

새로운 Y는 R1부터 R5 사이의 집합 가운데 속할 것이다 각 관측치는 Y의 값을 가지고 있다고 하였다, 그것을 이용하여 새로운 관측치에 대한 Y를 예측할 수 있다. 새로운 Y가 어떤 부분집합에 속할지 결정하는 것이 의사결정트리이다.

왼 쪽 방법으로의 표현은 변수가 최대 3개라면 시각적으로 표현하기 쉽다. 하지만 4개 이상이 되면 차원이 4차원 이상이 되므로 표현이 쉽지 않다. 그렇기 때문에 오른쪽의 의사결정트리 모델을 도식화한 형태로 보는 것이 훨씬 편리하다.
데이터의 총 합은 예측나무모델에서 Leaf Node에 포함된 관측치의 개수와 같다.
예측 의사결정나무 모델링 프로세스
1. 데이터를 M개로 분할 :
2. 최상의 분할은 비용함수(cost function)를 최소할 때 얻어진다.
3. 각 분할에 속해 있는 y 값들의 평균으로 예측했을 때 오류가 최소
그렇다면 분할변수
노드의 분리 기준은 마디의 순수도는 증가하고 불순도는 감소하는 방향으로 분류를 진행해야 한다. 이 방법에 대해서는 분류 의사결정나무 까지 정리한 이후에 설명하려 한다.
분류 의사결정나무
분류는 비슷한 범주를 갖고 있는 관측치끼리 모으는 방향으로 의사결정나무 모델을 만들어 나간다.
아래 그림을 예시로 들어보자. 관측치가 2개의 색 빨강, 초록이 혼합되어 있는 것을 볼 수 있다. 이것의 분류를 나누다 보면 오른쪽과 같이 분류할 수 있을 것 같다.
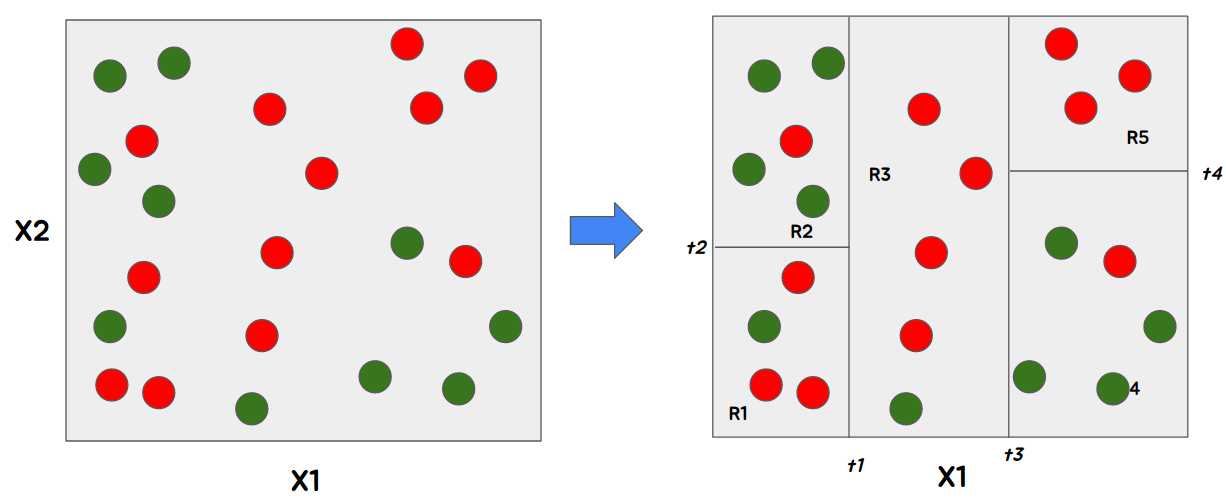
이때, 새로운 관측치가 R4로 분류가 되었다면, 당신은 이 관측치를 무슨색으로 판단하겠는가? 당연히 초록색으로 분류를 할 것이다.
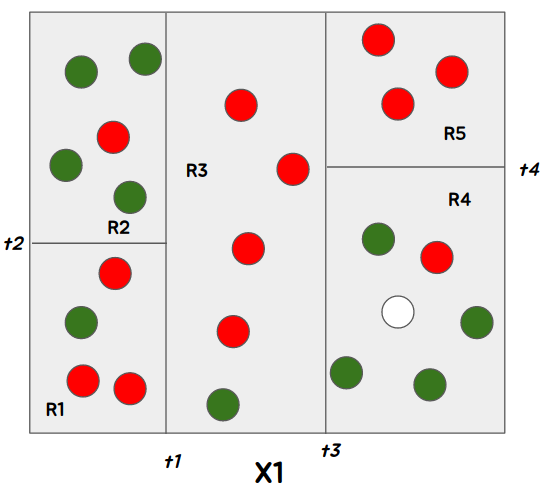
R4 영역 자체에 초록색이 대다수 이기 때문에 초록색일 확률이 높을것이기 때문이다. 이러한 분류를 의사결정나무 모델을 도식화한다면 아래와 같은 그림이 될 것이다.
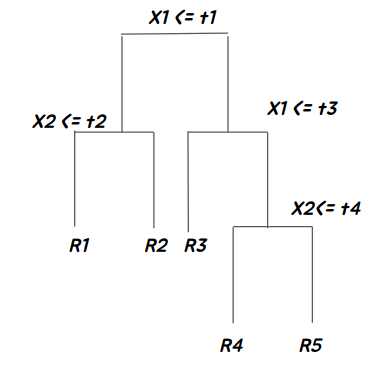
분류모델에서의 비용함수 (불순도 측정)
분류 모델 에서의 비용함수는 불순도 측정을 사용한다. 불순도라는 단어는 잘 생각하면 순수한 어떤 물체에 얼마나 불순물이 섞여있는지에 대한 수치화로 이해할 수 있다. 불순도는 의사결정나무에서 분기 기준을 선택하기 위해 사용한다.
불순도는 복잡성을 의미하고 해당 범주안에 서로 다른 데이터가 얼마나 섞여있는지를 뜻한다. 다양한 Feature들이 섞여 있을수록 불순도는 높다. 이러한 불순도를 이용하여 분기는 현재 노드의 불순도 보다 자식 노드의 불순도가 낮아야 하며, 이 불순도의 차이를 Information Gain이라고 한다. (Information Gain은 뒤에서 다시 다룬다.)
불순도 측정에 사용하는 방식은 크게 3가지 이다.
- Gini Index (지니계수)
- Cross-entropy (엔트로피)
- Miclassification rate (오분류율)
지니 계수
크로스 엔트로피
엔트로피는 의사결정나무의 성능을 평가하기 위해 사용되는 개념이다. 무질서라는 개념으로 일반인들에게 더 자주 사용된다. 여기서 엔트로피는 불순도(Impurity)로 표현한다.
즉, 분류한 모델에 잘못 분류된 관측치가 얼마나 속해있는지로 불순도 계산이 가능하다.
분류 의사결정나무 모델링 프로세스
분할법칙
- 분할변수와 분할기준은 목표변수의 분포를 가장 잘 구별해주는 쪽으로 결정한다.
- 목표변수의 분포를 잘 구별해주는 측도로 순수도 또는 불순도를 정의한다.
- 예를들어 클래스 0과 클래스 1의 비율이 45%와 55%인 노드는 각 클래스의 비율이 90%와 10%인 마디에 비하여 순수도가 낮다고 해석할 수 있다.
- 각 노드에서 분할변수와 분할점의 설정은 불순도의 감소가 최대가 되도록 선택한다.
즉 다시 말해 불순도를 감소시키는 방향으로 분할을 하게 된다. 그 순서는 아래와 같다.
- 모든 데이터를 포함한 루트노드로 부터 시작
- 데이터 중 불순도를 낮추는 최적의 요인을 탐색
- 루트 노드를 최적의 요인의 기준값을 찾아 하위 그룹으로 분할한다
- 각 하위 그룹에 대한 의사결정나무의 노드를 생성한다
- 반복적으로 새로운 하위 노드에서 최적의 요인과 기준값을 찾고 하위 그룹을 만든 후 각 하위 그룹에 대한 의사결정나무의 노드를 만든다. (3 ~ 4 반복)
- 위 과정을 더 이상 노드를 나눌 수 없을 때 까지 혹은 정지 규칙에 도달할 때 까지 반복한다.
의사결정나무의 장단점
장점
- 시각화를 통한 해석의 용이성
- 나무 구조로 표현되어 이해가 쉬움
- 새로운 개체 분류를 위해 루트 노드부터 끝 노트까지 따라가면 되므로 분석 용이
- 데이터 전처리, 가공작업이 불필요 (상대적으로)
- 수치형, 범주형 데이터 모두 적용 가능
- 비모수적인 방법으로 선형성, 정규성 등의 가정이 필요없고 이상값에 민감하지 않음
- 대량의 데이터 처리에도 적합하고 모형 분류 정확도가 높음.
단점
- 휴리스틱에 근거한 실용적 알고리즘으로 학습용 자료에 의존하기에 전역 최적화를 얻지 못할 수도 있음
- 검증용 데이터를 활용한 교차 타당성 평가를 진행하는 과정이 필요
- 자료에 따라 불안정함
- 적은 수의 자료나 클래스 수에 비교하여 학습 데이터가 적으면 높은 분류에러 발생
- 각 변수의 고유한 영향력을 해석하기 어려움
- 자료가 복잡하면 실행시간이 급격하게 증가함
- 연속형 변수를 비연속적 값으로 취급하여 분리 경계점에서는 예측오류가 매우 커지는 현상 발생
의사결정나무 분류 모델 단순 예제
Import library
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import f1_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_reportLoad dataset
raw_wine = datasets.load_wine()
X = raw_wine.data
y = raw_wine.targetSplit train and test data
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=123)Scaling dataset
scaler = StandardScaler().fit(X_train)
X_train_ss = scaler.transform(X_train)
X_test_ss = scaler.transform(X_test)Train DecisionTree Model
model = DecisionTreeClassifier(random_state=123).fit(X = X_train_ss, y = y_train)Prediction
pred = model.predict(X_test_ss)Check result
print(f1_score(y_test, pred, average = 'macro'))
print(confusion_matrix(y_test, pred))
print(classification_report(y_test, pred))0.9433862433862433
[[14 0 0]
[ 1 17 0]
[ 1 1 20]]
precision recall f1-score support
0 0.88 1.00 0.93 14
1 0.94 0.94 0.94 18
2 1.00 0.91 0.95 22
accuracy 0.94 54
macro avg 0.94 0.95 0.94 54
weighted avg 0.95 0.94 0.94 54참고
김성범 교수님 - 머신러닝 | 의사결정나무 (https://www.youtube.com/watch?v=2Rd4AqmLjfU&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=22)
'AI > Machine Learning' 카테고리의 다른 글
| 데이터 불균형 - Over Sampling (1) | 2023.09.24 |
|---|---|
| 데이터 불균형 - Under Sampling (1) | 2023.09.24 |
| 정규화 모델 (Regularization Model)의 기본 원리 (0) | 2023.04.01 |
| [Machine Learning] 차원축소 - #1 PCA (0) | 2023.03.27 |
| [Agent] Software Agent Architecture (0) | 2018.10.28 |
