
데이터 분석 및 기계학습을 위해 데이터를 수집하다보면 데이터의 정상 범주의 관측치 수와 이상 범주의 관측치 수의 차이가 크게 나타나는 경우를 만날 수 있다. 이와 같은 상황은 매우 빈번하게 마주할 수 있다.
이러한 데이터 불균형은 왜 문제가 되는가? 우리는 데이터를 기반으로 정상을 정확하게 분류하는 것과 이상값을 정확히 분류하는 문제로 크게 나뉠 수 있다. 보통 정상인 데이터들이 다수이며 이상값이 소수이다. 일반적으로 정상을 분류하는 것보다 이상값을 분류하는 것이 더 중요한 문제로 다뤄진다.
이렇게 클래스 별로 관측치의 수가 현저하게 차이가 나는 데이터를 불균형 데이터라고 하며, 이러한 상황을 해결하기 위한 방법들을 간략하게 정리한다.
데이터 불균형을 해결하기 위한 방법은 Data-based 접근 방식과 Modeling-based 접근방식이 존재한다. 이 글에서는 Data-based 접근방식만 정리한다. Data-based 접근 방법은 크게 아래와 같이 Under-sampling, Over-sampling 2가지로 나뉘며 각 샘플링 기법내에 다양한 방법들이 존재한다.
- Under-sampling
- Random undersampling
- Tomek links
- Condensed NEarest Neighbor Rule (CNN)
- One-sided selection (Tomek links + CNN)
- Over-sampling
- Resampling
- SMOTE
- Borderline-SMOTE
- ADASYN
- MCMC (Markov Chain Monte Carlo)
이 글에서는 Under Sampling에 대해 정리한다. Over Sampling을 정리한 글은 아래 글을 참고하길 바란다.
2023.09.24 - [AI/Machine Learning] - 데이터 불균형 - Over Sampling
데이터 불균형 - Over Sampling
데이터 분석 및 기계학습을 위해 데이터를 수집하다보면 데이터의 정상 범주의 관측치 수와 이상 범주의 관측치 수의 차이가 크게 나타나는 경우를 만날 수 있다. 이와 같은 상황은 매우 빈번하
sonseungha.tistory.com
Under Sampling
Under Sampling의 철학은 다수 범주의 데이터를 줄여서 소수 범주와 유사하게 만들어 각 범주의 데이터 수를 비슷하게 함으로써 분류 성능을 올리는 것이다.

1) Random Undersampling
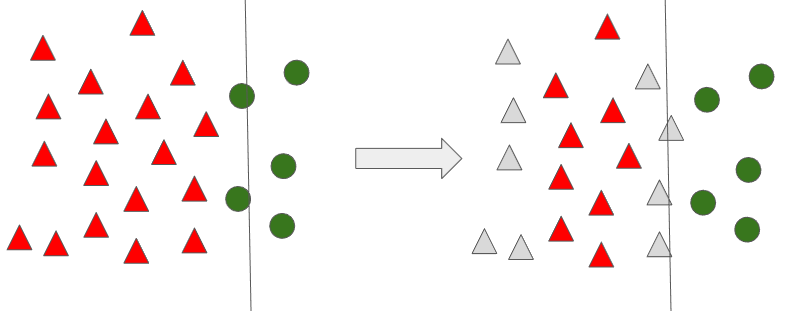
아주 단순한 방법이다. 다수 범주에 속해있는 관측치를 삭제하여 소수 범주와의 데이터 수 밸런스를 맞추는 방식이다. 이 때 삭제하는 데이터의 선별은 랜덤하게 선별한다.
이 방법의 문제는 어떻게 데이터를 선택하느냐에 따라 경계가 변경될 수 있다는 것이다.

위 그림처럼 샘플링 할때마다 성능이 달라질 수 있다.
2) Tomek links
Tomek links는 두 개의 데이터 Pair
위의 설명을 간략하게 정리하면 아래 그림과 같이

그렇다면 Tomek links가 무엇인가? 두 점 사이의 거리가 최소가 되는 Pair

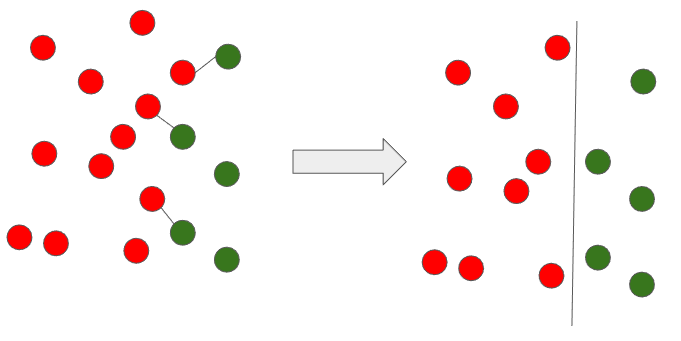
위와 같은 방식으로 데이터 셋에서 모든 Tomek links를 찾고 다수 범주에 속한 관측치를 제거하는 방법이 Tomek links 기법이다. 아래와 같이 Tomek links에 해당하는 데이터는 경계값이므로 제거 시 좀 더 명확하게 다수와 소수 범주의 데이터를 분류할 수 있는 것을 알 수 있다.
3) Condensed Nearest Neighbor Rule (CNN)
CNN 기법은 소수 범주 데이터 전체와 다수 범주에서 무작위로 하나의 관측치를 선택하여 서브 데이터를 구성합니다. 그 이후 다수 범에서 선택한 하나의 관측치를 제외한 나머지 데이터를 1-Nearest Neighbor 기법을 통해 샘플링할 데이터를 선정하는 방식입니다.
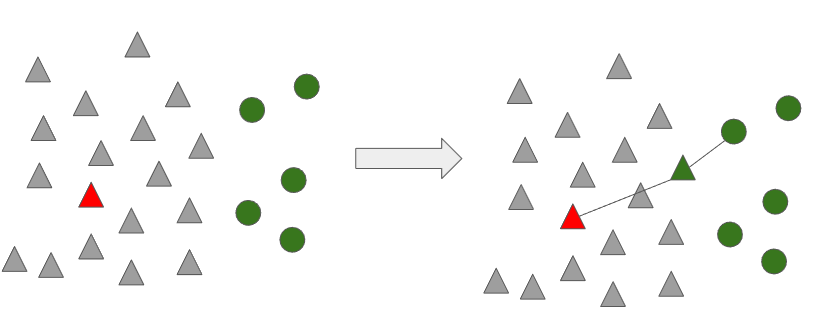
아래 그림처럼 다수 범주 데이터에서 무작위로 하나의 데이터를 선택합니다.

선택받지 못한 다수 범주의 데이터들을 이용하여 1-Nearest Neighbor 기법을 통해 거리를 계산하고 가까운 쪽으로 범주를 변환합니다.
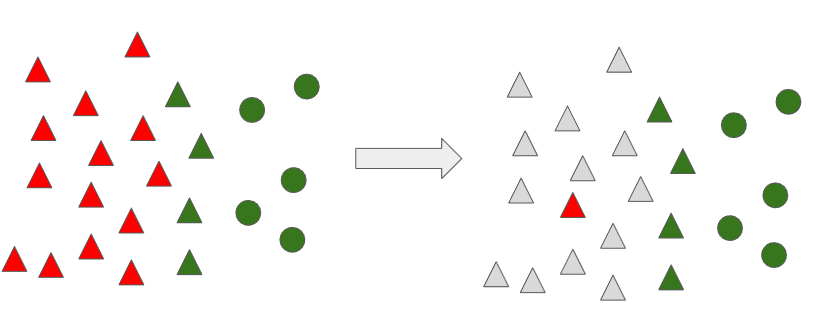
모든 데이터에 대해 위 과정을 반복 수행하게 되면 아래와 같이 나타나게 되고, 다수 범주 데이터로 분류된 관측치를 제거합니다.
이 과정이 완료되면, 아래와 같이 처음에 경계선이 좀 더 명확하게 분류를 할 수 있도록 조정 되는 것을 알 수 있습니다. 이러한 방법이 Condensed Nearest Neighbor Rule (CNN) 입니다.
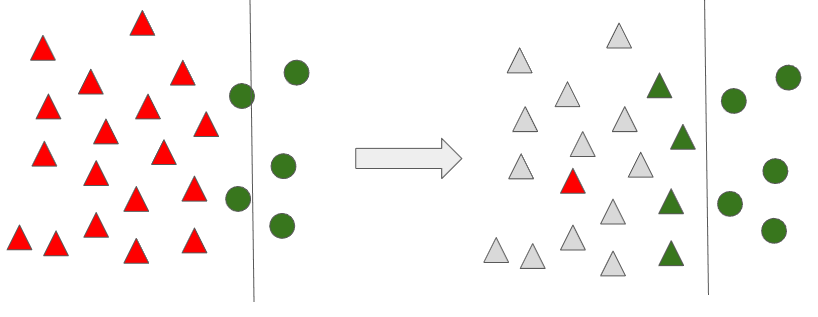
여기서 주의할 점은 다수 범주의 분류를 위해 1-Nearest Neighbor 기법을 사용해야 한다는 것입니다. K가 1이 아닌 3, 5 등의 수는 무조건 소수 범주로 분류가 됩니다. 다수 범주 중 딱 하나의 데이터만 뽑았기에, K가 1이 아니라면 문제가 발생합니다. 이 점 주의하시기 바랍니다.
4) One-Sided Selection (Tomek links + CNN)
One-Sided Selection(이하 OSS) 은 Tomek links와 CNN 기법을 합친 방법이다.
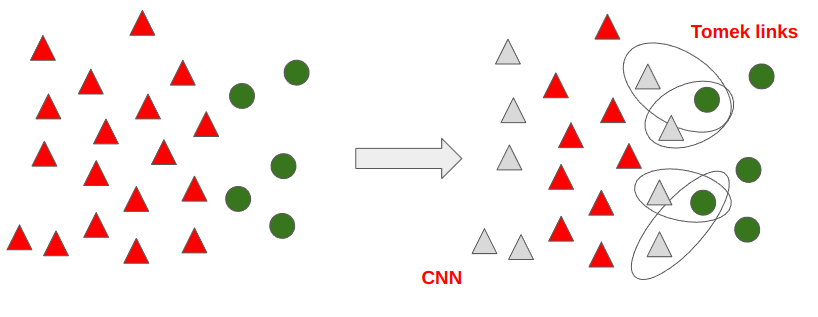
Tomek links 로 Pair 된 데이터 중 다수 범주에 속하는 데이터를 삭제하고, CNN을 통해 데이터를 함께 삭제하게 되면 아래의 데이터만 남게되고, 분류 경계선이 더욱 명확해 짐을 알 수 있다.
5) 정리
- 장점
- 다수 범주에 속하는 데이터를 없앰으로써 전체 데이터 수가 줄어들어 계산 시간이 감소한다.
- 데이터 클랜징으로 클래스 오버랩 감소 기능이 있다.
- 단점
- 데이터 제거로 인한 정보 손실이 발생한다.
참고
김성범 교수님 강의 자료 - https://www.youtube.com/watch?v=Vhwz228VrIk&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=17
'AI > Machine Learning' 카테고리의 다른 글
| 이상치 탐지(Anomaly Detection) - Overview (0) | 2023.10.28 |
|---|---|
| 데이터 불균형 - Over Sampling (1) | 2023.09.24 |
| 의사결정 나무 (Decision Tree) 예측, 분류 정리 (0) | 2023.04.01 |
| 정규화 모델 (Regularization Model)의 기본 원리 (0) | 2023.04.01 |
| [Machine Learning] 차원축소 - #1 PCA (0) | 2023.03.27 |
