
차원축소 (Dimension Reduction)
데이터에는 중요한 정보와 중요하지 않은 정보가 함께 혼재되어 있다. 여기서 우리는 중요하지 않은 정보를 노이즈(Noise) 라고도 부른다. 이런 노이즈들은 우리가 데이터에서 유의미한 결과를 분석하기 위한 과정에 방해가 되는 요소이다. 데이터분석, 기계학습분야에서는 이러한 노이즈를 제거하는 것이 매우 중요한 과제 중 하나이다.
데이터 표본의 수와 변수가 매우 많으면 데이터 분석 과정에서 데이터를 파악하는 일이 매우 어렵다. 이러한 문제를 해결하기 위해 제시된 것이 차원 축소이다.
차원축소는 고차원의 데이터를 저차원의 데이터로 변환하는 과정이다. 차원은 간단하게 말해 데이터 분석 측면에서 하나의 차원이 하나의 변수로 이해하면 쉽다. 변수의 수가 늘어나게되면, 차원이 커지면서 차원의 저주 문제가 발생한다.여기서 차원의 저주란 데이터의 양에 비해 차원이 많아지면서 복잡함이 발생하고 그에 따라 과적합 문제로 이어지게 된다. 이러한 과적합 문제 해소와 시각화의 용이성을 확보하기 위해 차원을 축소한다.
차원 축소 기법에는 PCA, Kernel PCA, LLE, LDA 등 다양한 기법이 있다. 그 중 PCA 에 대해서 이 글에서 정리하고자 한다. 차원 축소 기법 PCA를 정리하기 앞서 차원의 저주에 대해 먼저 정리한다.
차원의 저주 (Curse of Dimensionality)
차원축소를 하는 가장 큰 이유 중 하나가 차원의 저주 문제를 해결하기 위함이다. 차원의 저주란 데이터의 차원이 커질수록 해당 차원을 표현하기 위해 필요한 데이터가 기하급수적으로 많아짐을 의미한다.
n 차원에서 n+1 차원으로 증가 시 필요로 하는 데이터는 기하급수적으로 증가하게 된다. 이러한 필요로 하는 데이터의 증가는 차원을 제대로 설명하지 못하게 된다. 차원을 설명하기 위해서는 데이터가 기하급수적으로 필요로 하게 되기 때문이다. 그에 따라 차원을 제대로 설명하지 못한 결과는 모델의 과적합(Over-Fitting)으로 이어지게 된다.
예를 들어 1차원을 10개의 데이터로 표현할 수 있다고 가정하자. 1차원에서 2차원으로 차원이 늘어나면 2차원 공간을 표현할 수 있는 데이터의 수는 100개가 필요하다. 이러한 차원이 3,4,...N 까지 늘어나게되면 필요로하는 데이터 수는 무한히 증가할 것이다.

차원축소는 위 같은 차원의저주 문제를 해결할 수 있다. 그 해결방법 중 하나인 PCA를 정리한다.
주성분 분석 (PCA, Princial Component Analysis)
주성분 분석 (이하, PCA)은 데이터셋의 차원을 축소하지만, 가능한 많은 정보는 유지하고자 하는 차원 축소 기법이다. PCA가 차원을 축소하는 방법을 간략히 정리하면, 서로 상관관계가 있는 변수를 찾아 정보 손실을 최소화 하고 차원을 줄이는 방법이다.
PCA는 차원을 축소함으로써 가장 적은 수의 주성분을 사용하여 분산의 최대량을 설명한다. 이게 따라 표현되는 주성분변수는 변수 정보를 축약한 변수이며 PCA는 일부 주성분에 의해 기존 변수의 변동이 충분히 설명되는지 알고보는 분석 기법이다.
즉, N개의 변수가 존재하는 경우 이를 통해 얻은 정보를 M개의 변수로 요약하는 것이다.

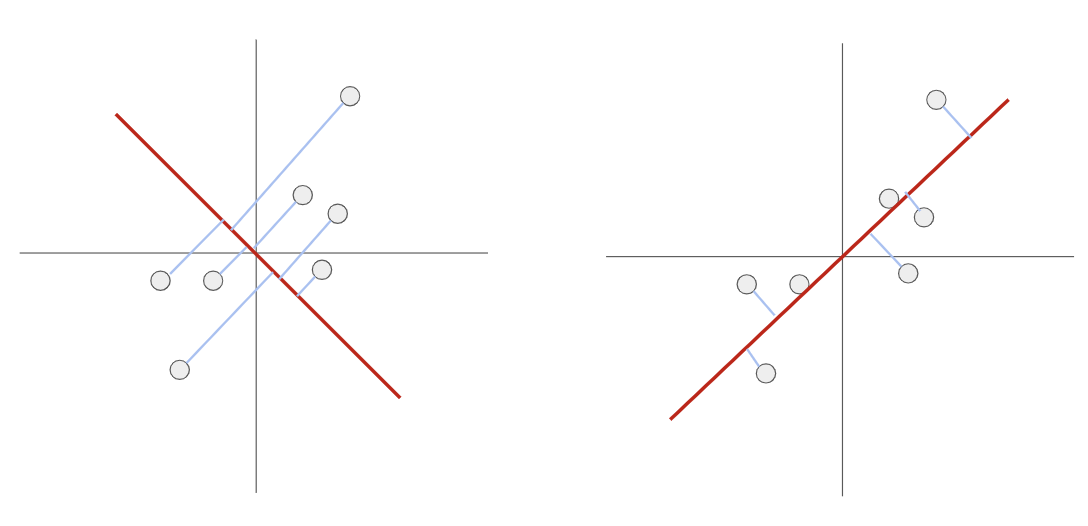
PCA는 데이터들을 위와 같이 정사영 시켜 차원을 낮추게 된다면, 어떤 벡터에 데이터들을 정사영 시켜야 원래의 데이터 구조를 잘 유지하면서도(데이터 손실의 최소화) 차원을 낮출 수 있는가에 대한 방법을 제공한다. 왼쪽보다는 오른쪽이 더 잘 표현해줄 수 있다.
PCA를 설명하기 위해서는 공분산행렬, 고윳값, 고유벡터등을 이해하고 수식적으로 확인하면 더 좋겠지만, 여기서는 간단한 이해와 코드만 확인하고 정리하려 한다. (수학적 정리와 설명은 다양한 블로그에서도 확인할 수 있다.)
주성분 분석(PCA) 알고리즘 순서
PCA는 아래의 과정을 통해 차원을 축소한다.
1. 변수간 상관관계 파악한다.
2. 공분산 행렬 구하기
3. 공분산 행렬의 고윳값과 고유벡터 구하기
4. 고윳값을 큰 순서대로 내림차순 정렬
5. d 차원으로 줄이고 싶은 경우, 크기 순서대로 d개의 고유값 선정
6. 선정한 고윳값에 대응하는 고유벡터로 새로운 행렬 생성
7. 처음 준비한 데이터를 6.에서 만든 새로운 공간으로 투영
상관관계를 파악한다면 변수 간의 공분산을 알 수 있다. 공분산 행렬을 통해 각 변수의 분산을 알 수 있고 변수 간 공분산도 알 수 있다. 이를 통해 상관계수도 파악할 수 있다. 행렬이란 선형변환이고 하나의 벡터공간을 선형적으로 다른 벡터 공간으로 매핑하는 기능을 가진다. 이때 데이터를 공분산 행렬을 적용하여 선형변환을 진행한다는 것은 아래와 같은 의미이다.
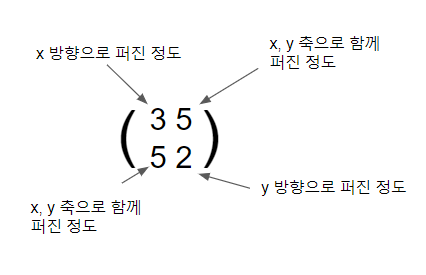
위에서 공분산행렬의 고윳값과 고유벡터를 구하는 이유는 고유 벡터를 통해 각 변수의 분산 방향을 알 수 있기 때문이며 고윳값은 분산의 크기를 알 수 있다. 즉 아래 그림에서 데이터가 여러 방향으로 흩어져 있을 때 고유 벡터를 이용하면 데이터의 흩어짐의 방향을 파악할 수 있고 어느정도 흩어졌는지 파악이되어 어떤 벡터로 투영을 시켜야 가장 데이터를 잘 표현할 수 있을지 알 수 있게 된다.
PCA외의 Kernel PCA, LLE 등은 다음 글로 정리한다.
참고자료
선형대수와 통계학으로 배우는 머신러닝 with 파이썬 | 장철원
https://angeloyeo.github.io/2019/07/27/PCA.html
'AI > Machine Learning' 카테고리의 다른 글
| 의사결정 나무 (Decision Tree) 예측, 분류 정리 (0) | 2023.04.01 |
|---|---|
| 정규화 모델 (Regularization Model)의 기본 원리 (0) | 2023.04.01 |
| [Agent] Software Agent Architecture (0) | 2018.10.28 |
| [Agent] Communication (0) | 2018.10.28 |
| [Agent] MAS (Multi-agent System) (0) | 2018.10.28 |
![[Machine Learning] 차원축소 - #1 PCA](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FugwhA%2Fbtr2zm8x9Yb%2FGxencJbzK5vYmcHy29Ldn1%2Fimg.png)