데이터 불균형 - Over Sampling

데이터 분석 및 기계학습을 위해 데이터를 수집하다보면 데이터의 정상 범주의 관측치 수와 이상 범주의 관측치 수의 차이가 크게 나타나는 경우를 만날 수 있다. 이와 같은 상황은 매우 빈번하게 마주할 수 있다.
이러한 데이터 불균형은 왜 문제가 되는가? 우리는 데이터를 기반으로 정상을 정확하게 분류하는 것과 이상값을 정확히 분류하는 문제로 크게 나뉠 수 있다. 보통 정상인 데이터들이 다수이며 이상값이 소수이다. 일반적으로 정상을 분류하는 것보다 이상값을 분류하는 것이 더 중요한 문제로 다뤄진다.
이렇게 클래스 별로 관측치의 수가 현저하게 차이가 나는 데이터를 불균형 데이터라고 하며, 이러한 상황을 해결하기 위한 방법들을 간략하게 정리한다.
데이터 불균형을 해결하기 위한 방법은 Data-based 접근 방식과 Modeling-based 접근방식이 존재한다. 이 글에서는 Data-based 접근방식만 정리한다. Data-based 접근 방법은 크게 아래와 같이 Under-sampling, Over-sampling 2가지로 나뉘며 각 샘플링 기법내에 다양한 방법들이 존재한다.
- Under-sampling
- Random undersampling
- Tomek links
- Condensed NEarest Neighbor Rule (CNN)
- One-sided selection (Tomek links + CNN)
- Over-sampling
- Resampling
- SMOTE
- Borderline-SMOTE
- ADASYN
- MCMC (Markov Chain Monte Carlo)
이 글에서는 Over Sampling에 대해 정리한다. Under Sampling을 정리한 글은 아래 글을 참고하길 바란다.
2023.09.24 - [AI/Machine Learning] - 데이터 불균형 - Under Sampling
데이터 불균형 - Under Sampling
데이터 분석 및 기계학습을 위해 데이터를 수집하다보면 데이터의 정상 범주의 관측치 수와 이상 범주의 관측치 수의 차이가 크게 나타나는 경우를 만날 수 있다. 이와 같은 상황은 매우 빈번하
sonseungha.tistory.com
Over Sampling
Over Sampling의 철학은 소수 범주의 데이터를 늘려서 다수 범주와 유사하게 만들어 각 범주의 데이터 수를 비슷하게 함으로써 분류 성능을 올리는 것이다.
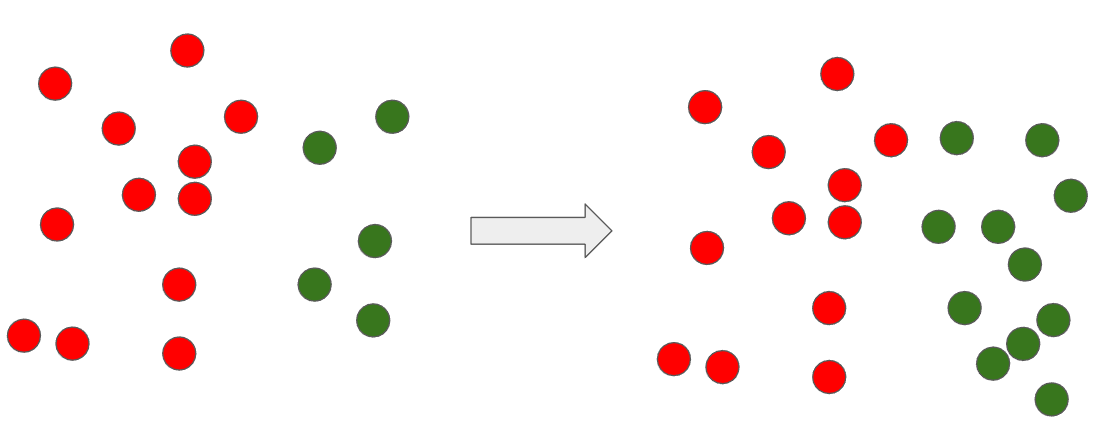
1) Resampling
Over sampling 기법 중 가장 간단한 방법이다. 소수 관측치를 다수 관측치의 수만큼 Resampling 하는 것이다. 즉 데이터 값이 동일한 중복된 데이터만 다수 만들어 놓는 방법이다.
단순하면서 무식한 방법이다. 이 방법은 소수 범주의 중복된 데이터들로 인해 Over-fitting이 쉽게 발생할 수 있다. 이러한 문제는 중복된 값을 만드는 것이 아닌 가상의 관측 데이터를 만들어내서 해결해야 한다. 앞으로 소개할 방법들이 이러한 방법이다.
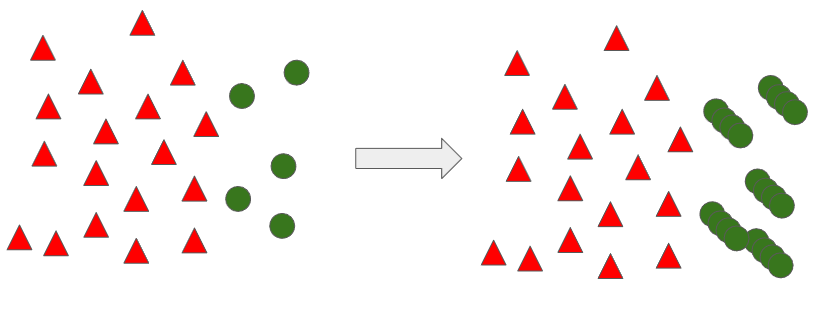
2) SMOTE (Synthetic Minority Oversampling TEchnique)
SMOTE 기법은 가상의 관측데이터를 생성하는 Over-Sampling 기법 중 하나이다. 아이디어는 단순하지만 매우 유명한 방법이다. 이 기법의 향상된 방안들이 지속적으로 개발되고 있다.
SMOTE는 소수 범주에서 가상 데이터를 생성할 때 K를 설정한다. 아래 예제는 K를 3으로 한다.
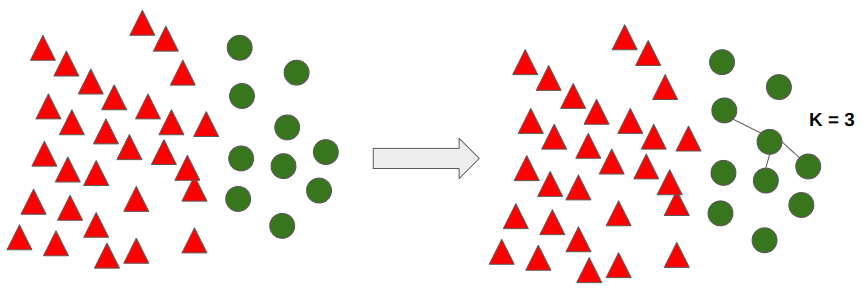
SMOTE 기법에서 K = 3인 개수를 선택하고 아래의 수식을 이용하여 가상의 데이터를 추가 생성한다.
$${ s = x + u \cdot (x^R - x)}$$
$x$ 는 위 그림에서 임의로 선택한 데이터이며, $x^R$은 Nearest Neighbor 관측치이다. Nearest Neighbor 관측치 중에 또다시 하나의 값을 무작위로 선정하게 된다. $u$는 균등분포로 0과 1사이의 랜덤 값이다. 이 수식을 이용해서 랜덤 데이터 $s$를 생성한다.

위 그림에서 처럼 특정 값의 K가 3인 Nearest Neighbor 값들을 찾고, 그 값 중 랜덤하게 하나를 선정한다. 그 이후 수식에 대입하여 가상의 데이터를 생성하게 된다. SMOTE 수식을 통해 각 데이터 간 0~1 사의 균등분포 랜덤 값만큼의 데이터가 생성된다. 이러한 방식으로 데이터가 증가한다.
SMOTE 기법 사용 시 주의할 점은 K는 1이여서는 안된다. K를 1로 설정하게 되면 Nearest Neighbor는 하나이고 무조건 해당 데이터 간 직선내에서 만 데이터가 생성된다.
3) Borderline SMOTE
Borderline SMOTE는 SMOTE 기법의 확장 기법 중 하나이다. Borderline은 경계선을 의미한다. 이 기법은 OverSampling을 소수 관측치 군집 내에서 하는 것 보다는 경계선에 위치한 소수 관측치들을 이용하여 OverSampling하는 것이 더 효율적이고 좋은 성능을 내지 않을까란 아이디어에서 출발한다.
- 소수 클래스 $x_{i}$에 대해서 K개 주변을 찾고, K 개 중 다수 클래스의 수를 확인한다.
- K 개의 관측치 중 다수 클래스의 관측치의 개수마다 Danger인지, Safe 인지, Noise 인지 판단한다.
- k = k` : Noise
- k/2 < k` < k : Danger 관측치
- 0 <= k` <= k/2 : Safe 관측치
- Danger 관측치에 대해서만 SMOTE를 적용한다.
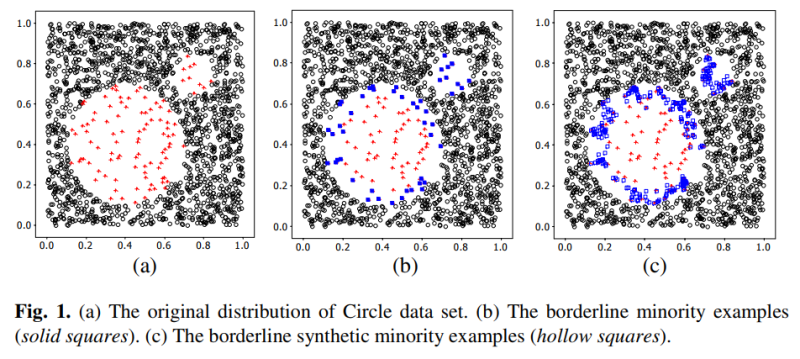
위 알고리즘을 통한 결과를 아래 그림으로 확인해보면, 경계선에 존재하는 Border line 관측치들 주변에만 새로운 데이터가 생성된 것을 확인할 수 있다.
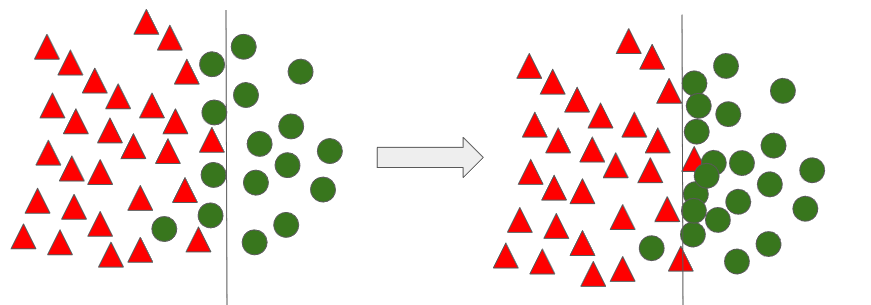
실제로 Border line SMOTE를 제안한 논문에서 예시 그림을 인용하면 아래와 같다. 더욱 명확하게 경계선에 가상의 데이터가 생성된 것을 확인할 수 있다.
4) ADASYN (Adaptive Synthetic Sampling Approach)
ADASYN은 Borderline Sampling 기법과 유사한데, 차이점은 샘플링하는 개수를 소수 관측치의 위치에 따라 다르게 수행하자라는 것이 주 아이디어이다.
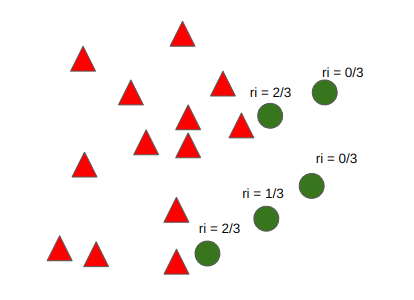
$${r_{i} = \Delta_{i} / K , i = 1,...,m}$$
${r_{i} $ : 각 소수 클래스 데이터 주변에 위치한 다수 클래스 데이터 개수의 크기를 정량화한 값
$\Delta_{i}$ : 소수 클래스 $x_{i}$의 주변 K 개 중 다수 클래스의 관측치 개수
$m$ : 소수 클래스 내 관측치 총 개수
위 수식의 의미는 각 소수 클래스 주변에 얼마만큼 많은 다수 클래스 관측치가 있는가를 정량화한 지료를 의미한다. 이를 통해 Borderline SMOTE와 유사하지만 다른 가상의 데이터를 만들어 낸다.
이렇게 만든 $r_{i}$ 값을 스케일링 한다. 스케일링은 $r_{i}$을 다 더한 값을 이용하여 $r_{i}$를 나눈 값이다. 이 값을 이용하여 새로 생성할 가상 데이터의 개수를 정의한다. 이 때 G 값을 정의하는데 G는 다수 클래수 개수 - 소수 클래스 개수이다. 여기서는 계산 편의상 G = 10 을 이용한다.
| 데이터 i | $r_{i}$ | $r_{i}$ Scaling 값 | Scaling x G |
| 1 | 0 | 0 | 0 |
| 2 | 2/3 | 0.4 | 4 |
| 3 | 0 | 0 | 0 |
| 4 | 1/3 | 0.2 | 2 |
| 5 | 2/3 | 0.4 | 4 |
이 과정을 통해 나온 개수 만큼 SMOTE를 통해 가상 데이터를 생성하게 된다.
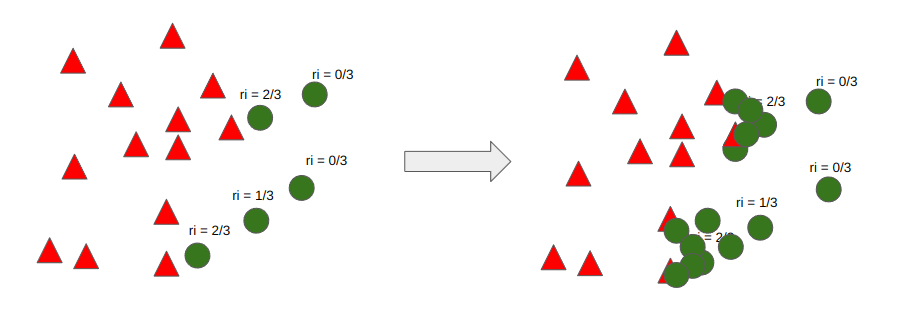
Borderline SMOTE와 다른 점은 경계선에 집중하는 것이고, ADASYN은 경계선 + 다수 클래스에 근접해 있는 소수 클래스 더욱 집중하자라는 것에 차이가 있다.
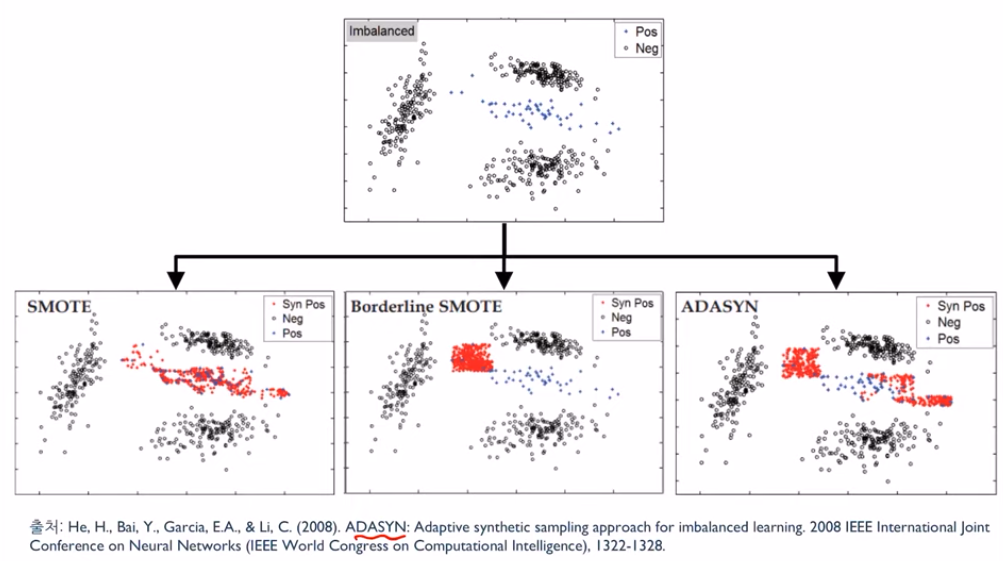
아래 이미지는 불균형 데이터를 SMOTE, Borderline SMOTE, ADASYN을 비교한 것이다. ADASYN이 무조건 SMOTE, Borderline SMOTE보다 잘 동작하는 것은 아니다. 아래 이미지는 ADASYN의 성능을 우수하게 보여주기 위한 특정 데이터이다. 해당 데이터는 다수 클래스의 범주가 여러개인 경우에 SMOTE, Borderline SMOTE보다 ADASYN의 성능이 좋음을 보여준다.
5) Markov Chain Monte Carlo (MCMC)
MCMC는 통계적인 특성을 이용하여 다양한 방식을 시도해보는 기법이다. MCMC 에서는 가장 마지막에 선정된 샘플이 다음 샘플을 추천해 준다는 아이디어에서 시작한다. 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에만 영향을 받는 확률 과정을 의미한다.
MCMC는 아래 단계를 거친다.
- Random initialization
- 제안분포 g(x)로 부터 다음 데이터 추천받기
- 패자부활전
- 위 2, 3단계를 지속 반복
(1) Random Initilization
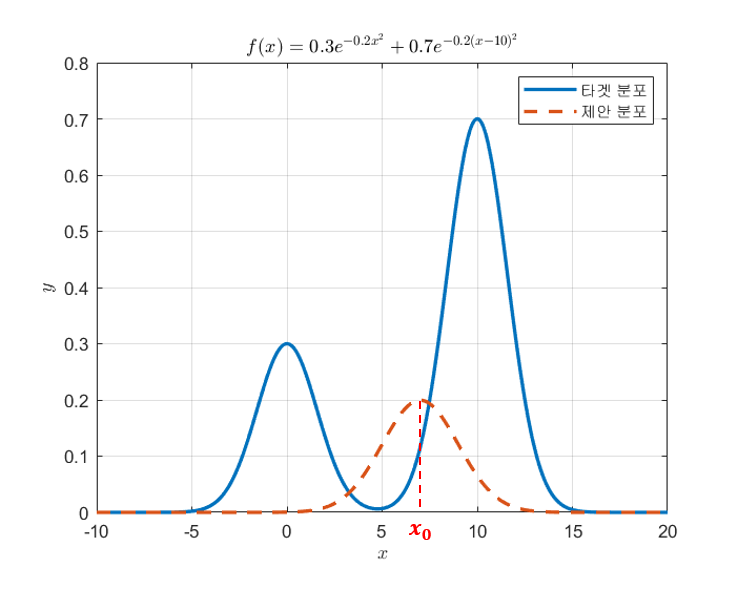
Random initialization은 데이터 샘플 공간에서 랜덤 값 하나를 입력하는 것이다. 여기서는 0.7인 값을 랜덤 값으로 사용한다.
(2) 제안 분포 g(x)로 부터 다음 데이터 추천받기
MCMC의 그 다음번 스텝은 제안 분포로부터 다음번으로 추출해볼 샘플을 추천받는 것이다. 여기서 제안분포는 라고 부르도록 하자. 처음 시작으로 잡은 $x_{0}$를 중심으로 정규분포를 하나 그려본다. 이 때, 정규분포의 너비(즉, 표준 편차)는 연구자의 선택에 따라 임의로 설정하면 된다. 이번 그림에서는 표준편차를 2로 설정해보았다.
만약 제안이 수용되었다면 수용된 샘플 포인트 $x_{1}$ 을 중심으로 제안 분포를 그리고, 이를 통해 샘픙을 또 추천 받는다. 만약 제안이 수용되지 않았다면 통계적으로 수용하게끔 MCMC는 패자부활전을 진행한다.
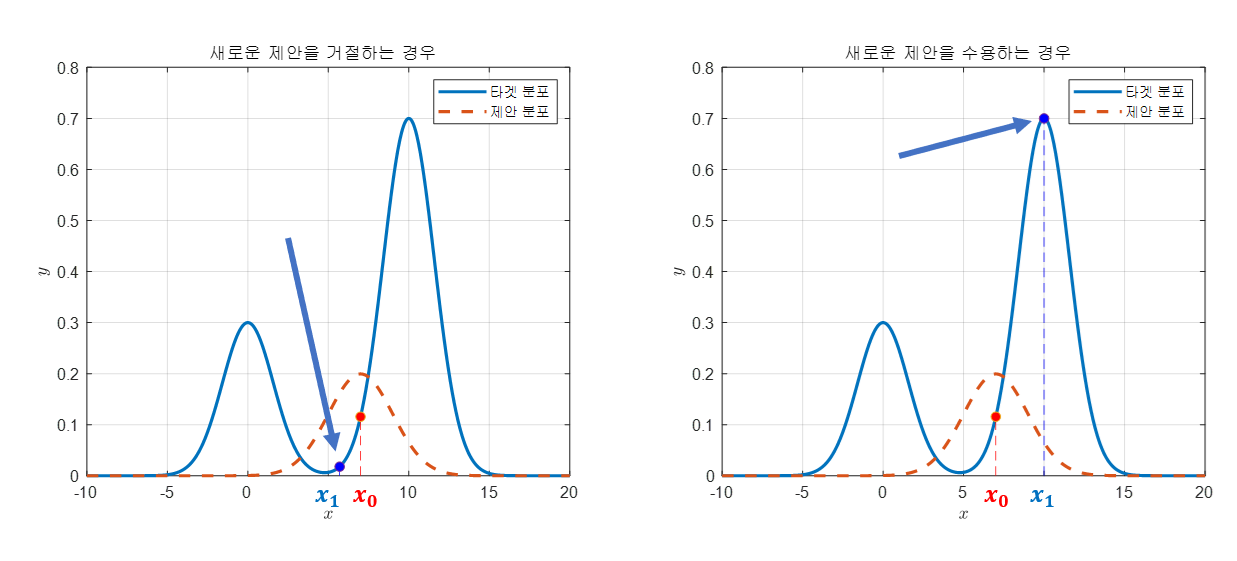
(3) 패자부활전
앞서 (2) 단계에서 거절된 샘플들은 무조건 이용하지 않는 것은 아니고, 통계적으로 수용할 수 있게 허용한다.
$${f(x_{1} / f(x_{2}) > u, u = uniform distribution U(0,1))}$$
만약 여기서도 위의 식을 만족하지 못한다면 그 때는 새로운 샘플 $x_{1}$을 샘플링하기를 수용하지 않고, $x_{1}$을 $x_{0}$로 설정한 뒤 다음 데이터 $x_{2}$를 추천받는다.
(4) 위 2, 3단계를 지속 반복
위 과정을 반복하며 데이터를 추천받고 생성을 한다.
6) 정리
- 장점
- Under Sampling과 다르게 정보 손실이 없다.
- 대부분의 경우 Under Sampling에 비해 높은 분류 정확도를 보인다.
- 단점
- 과적합 가능성
- 계산 시간이 증가
- 노이즈 또는 이상치에 민감
참고
https://angeloyeo.github.io/2020/09/17/MCMC.html
https://www.youtube.com/watch?v=Vhwz228VrIk&list=PLpIPLT0Pf7IoTxTCi2MEQ94MZnHaxrP0j&index=17