Time Series Data Augmentation for Deep Learning: A Survey

AI/Paper-Review

Time Series Data Augmentation for Deep Learning: A Survey

Linuxias 2024. 5. 6. 20:28

"Time Series Data Augmentation for Deep Learning: A Survey"는 딥러닝에서 시계열 데이터 증강에 대한 연구 동향과 적용 가능한 기법들을 상세히 조사한 논문입니다. 아래는 논문 내용의 상세한 설명입니다.

1. Introduction

1) paper Information

30th International Joint Conference on Artifical Intelligence(IJCAI 2021) Accepted Paper
Deep Learning 시계열 데이터 분석 전반에 사용될 수 있는 Data Augmentation 기법들을 정리한 논문
글 작성 시점 (2024. 05. 06) 기준으로 681회 인용된 논문

2) Backgrounds

딥러닝은 컴퓨터 비전, 자연어 처리 등의 연구 분야에서 큰 성과를 보이고 있습니다. 이러한 성과를 이룰 수 있었던 배경에는 우수한 딥러닝 모델들의 구조와 더불어 충분히 많은 데이터와 데이터 증강을 통해 모델이 과적합 됨을 방지하였기 때문입니다.

2.1) 컴퓨터 비전 분야의 Augmentation 기법 종류

컴퓨터 비전 분야에서는 다양한 데이터 증강 기법이 사용되어 모델의 성능을 향상시키고, 일반화 성능을 향상시키는 데 활용됩니다. 여러 가지 데이터 증강 기법 중 일부를 아래에 설명합니다:

이동(Translation):
- 이미지를 수평 또는 수직으로 이동시켜서 새로운 이미지를 생성하는 기법입니다. 이미지 내의 객체 위치 변화를 모방하고 데이터 다양성을 증가시키는 데 효과적입니다.
회전(Rotation):
- 이미지를 일정한 각도로 회전시켜 새로운 이미지를 생성하는 기법입니다. 회전은 이미지의 각도에 대한 불변성을 학습하고, 다양한 각도에서의 객체 인식을 향상시키는 데 도움이 됩니다.
확대/축소(Scaling):
- 이미지의 크기를 확대 또는 축소하여 다양한 크기의 이미지를 생성하는 기법입니다. 크기 변화에 대한 강인한 모델을 학습하고, 다양한 크기의 객체를 인식하는 데 도움이 됩니다.
밝기 조절(Brightness Adjustment):
- 이미지의 밝기를 조절하여 새로운 이미지를 생성하는 기법입니다. 밝기 변화에 대한 강인한 모델을 학습하고, 다양한 조명 조건에서의 객체 인식을 향상시키는 데 사용됩니다.
채도 조절(Saturation Adjustment):
- 이미지의 채도를 조절하여 다양한 색상의 이미지를 생성하는 기법입니다. 채도 변화에 대한 강인한 모델을 학습하고, 다양한 환경에서의 객체 인식을 향상시키는 데 도움이 됩니다.
가우시안 노이즈 추가(Gaussian Noise Injection):
- 이미지에 가우시안 노이즈를 추가하여 새로운 이미지를 생성하는 기법입니다. 노이즈에 강인한 모델을 학습하고, 다양한 환경에서의 객체 인식을 향상시키는 데 사용됩니다.
가로 뒤집기(Horizontal Flip):
- 이미지를 가로로 뒤집어서 새로운 이미지를 생성하는 기법입니다. 객체의 좌우 대칭 변화를 모방하고, 데이터 다양성을 증가시키는 데 효과적입니다.
세로 뒤집기(Vertical Flip):
- 이미지를 세로로 뒤집어서 새로운 이미지를 생성하는 기법입니다. 객체의 상하 대칭 변화를 모방하고, 데이터 다양성을 증가시키는 데 사용됩니다.

이 외에도 다양한 데이터 증강 기법들이 있으며, 이를 조합하여 모델의 학습을 더욱 효과적으로 할 수 있습니다.

2.2) 시계열 데이터 분석 분야의 데이터 증강(Augmentation)

시계열 데이터 분석 분야에서 딥러닝을 활용한 연구 분야는 많이 이뤄지고 있습니다.

TimeSeries Classification
TimeSeries Anamaly Detection
TimeSeries Forcasting

하지만 시계열 데이터 분석 분야서의 데이터 증강 관련 연구들은 컴퓨터 비전과 자연어처리와 같은 분야와 달리 활발하게 이뤄지지는 않고 있습니다. 해당 논문에서는시계열 데이터 분석에서의 데이터 증강 연구의 어려움을 아래와 같이 크게 2가지로 정리하고 있습니다.

한계점 1. 현존하는 데이터 증강 기법들은 시계열 데이터의 내재적 특성(Intrinsic property)을 활용하지 못함
- 일반적으로 시계열 데이터는 시간 종속성(Temporal Dependency)이라는 특성을 가집니다.
- 이미지나 언어 데이터와는 다르게 시계열 데이터는 크게 시간과 빈도 도메인으로 나눌 수 있는데, 이러한 각각의 Transformed Domain에 적합한 데이터 증강이 수행되어야 하기 때문에 다른 데이터에 비해 비교적 어려움이 있습니다.
한계점 2. 현존하는 데이터 증강 기법들은 Task에 의존적인 경향이 존재함
- TimeSeries Classification에 쓰인 증강기법이, TimeSeries Anomaly Detection에는 적합하지 않을 수 있습니다.
- 또한, 데이터 간의 불균형이 큰 데이터와 그렇지 않은 데이터를 활용함에 있어서 다른 접근의 Data Augmention이 필요할 수 있습니다.

2.3) 논문에서 제시하는 시계열 데이터 증강 기법의 분류

해당 논문에서는 시계열 데이터 증강 기법을 크게 Basic Approaches와 Advanced Approaches로 나뉠 수 있다고 제시하고 있습니다.

Basic Approaches에서는 시간, 주파수 영역에서의 증강 기법에 대해 설명하고 Advanced Approaches에는 확률적 기법이나 학습 기법을 활용한 데이터 증강 기법에 대해 분류하고 있습니다.

2. Basic Approaches

본 논문에서 분류하고 있는 Basic Approaches에는 Time Domain, Ferquency Domain, Time-Freq Domain 3가지로 분류하고 있습니다.

1) Basic Approaches의 분류

Time Domain, Ferquency Domain, Time-Freq Domain 분류 내의 종류는 아래와 같습니다.

Time Domain
- Window cropping, slicing
- Window warping
- Flipping
- Perturbation & Ensemble
- Noise Injection
- Label Expansion
Frequency Domain
- APP (Amplitude and Phase Pertubations)
- AAFT (Amplitude Adjusted Fourier Transform) & IAAFT(iterated AAFT)
Time-Frequency Domain
- STFT (Short Fourier Transform)
- Mel-Frequency

2) Time Domain

시간 영역 변환은 시계열 데이터에 대한 가장 직관적인 데이터 증강 방법 중 하나입니다. 대부분의 경우 이러한 방법들은 원래 입력 시계열 데이터를 직접 조작합니다. 가우시안 노이즈를 주입하거나 스파이크, 단계적 추세 및 기울기와 같은 더 복잡한 노이즈 패턴을 주입하는 것과 같은 방법입니다.

2.1) Window cropping, slicing

Window cropping, slicing기법은 컴퓨터 비전영역에서의 자르기와 유사합니다. 이는 원래 시계열 데이터에서 연속된 조각을 무작위로 추출하는 샘플링 방법입니다.

2.2) Window warping

Window warping 기법은 시계열 데이터를 위한 독특한 증강 기법 입니다. 동적 시간 왜곡(DTW)와 유사하게 무작위 시간 범위를 선택한 다음, 해당 범위를 압축(다운 샘플링)하거나 확장(업샘플링) 합니다. 다른 시간 범위는 변경되지 않습니다. Window warping은 원래 시계열의 총 길이를 변경하므로 딥러닝 모델에는 Window slicing과 함께 수행되어야 합니다.

https://towardsdatascience.com/time-series-augmentations-16237134b29b

2.3) Perturbation & Ensemble

Perturbation을 수행한 시계열 데이터에 대하여 DTW를 수행하여 Original data의 길이로 맞춰준 뒤 ensemble하는 DBA(DTW Barycentric Averaging)기법을 통해 데이터를 증강하는 기법입니다.

자세한 설명은 해당 링크를 (https://arxiv.org/pdf/1808.02455) 참고해주세요.

2.4) Noise Injection

시계열 데이터 원본에 Noise나 Outlier를 주입하는 방법입니다. Spike, Step-like Trand, Slope-like Trend 등의 기법등이 사용됩니다. 해당 노이즈는 Label의 정보가 변경되지 않는 매우 적은 값으로 설정해야 합니다.

2.5) Label Expansion

시계열 이상치 탐지의 경우 이상치들이 단순히 한 시점이 아니라 연속적으로 길게 나타나는 특성이 있습니다.(Blurry) 이에 단순 한 시점을 이상치로 하지 않고, Label Expansion을 통해 주변까지 이상치로 정의해주는 방법입니다. (https://arxiv.org/pdf/2002.09545)

3) Frequency Domain

주파수 영역에 대해 이해하기 위해서는 푸리에 변환(Fourier Transform)에 대해 간단히라고 이해하고 있어야 합니다. 푸리에 변환은 다양한 자료들을 구하기 쉽기에 건너뛰겠습니다.
(추천 자료 : https://angeloyeo.github.io/2020/11/08/linear_algebra_and_Fourier_transform.html)

주파수 영역은 시계열 데이터를 어떻게 주기로 표현할 수 있을까? 란 질문으로 시작합니다. 시계열 데이터를 얼마만큼의 크기로(진폭) 어느 위치에서 출발(위상)할지에 대해 나눠서 확인해볼 수 있습니다.

Amplitude Spectrum (진폭) : 시계열 데이터가 갖는 주파수 성분들의 진폭
Phase Spectrum (위상) : 각 주파수 성분들의 시간 축 상의 위치를 의미함.

위 내용을 기반으로 Frequency Domain에서 사용되는 APP, AAFT 기법에 대해 간략히 정리하겠습니다.

3.1) APP (Amplitude and Phase Perturbations)

앞서 소개했던 시계열 데이터의 Amplitude Spectrum과 Phase spectrum에 Perturbation을 수행한 기법입니다. Amplitude Spectrum은 일부 데이터를 원본 데이터의 평균과 분산을 갖는 Gaussian Noise로 대체하고 Phase Spectrum은 일부 데이터에 zero-mean Gaussian Noise를 더합니다.

3.2) AAFT (Amplitude Adjusted Fourier Transform) & IAAFT(iterated AAFT)

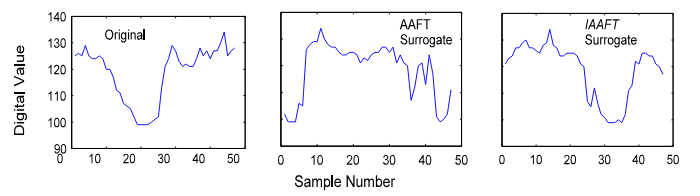
AAFT는 푸리에 변환 후 Phase Spectrum에서 무작위로 Phase를 Shuffle한 뒤 Inverse Fourier Transform을 수애하여 Amplitude는 보존되고 Phase만 바뀐 데이터를 생성하는 방법입니다. IAAFT는 AAFT의 발전된 버전으로, iterative step을 통해 AAFT가 좀 더 잘 수렴할 수 있도록 개선시킨 방법입니다. AAFT와 IAAFT 기법의 장점은 해당 기법들로 생성된 시계열 데이터는 대략적으로 기존 시계열 데이터의 시간 상관 관계, 전력 스펙트럼 및 진폭 분포 보존이 가능하는 것입니다.

4) Time-Frequency Domain

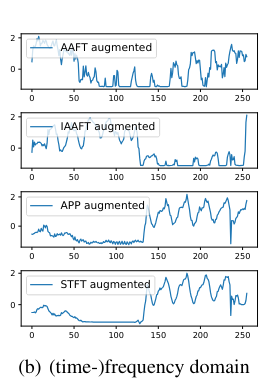
4.1) STFT (Short Fourier Transform)

STFT는 주파수 특성이 시간에 따라 달리지는 특징을 분석하기 위한 방법입니다. 즉 시계열 데이터를 시간 단위로 짧게 분할한뒤 FFT를 수행하는 방법입니다.

4.2) Mel Spectrogram

주파수의 단위를 특정 공식에 맞춰 멜 단위(Mel unit)으로 변경한 스펙트럼입니다. 청각이 저음의 주파수 변화에 민감하고 고음의 주파수 변화에 덜 민감한 특징을 사용하여 만들어진 기법입니다.

3. Advanced Approaches

1) Advance Approaches의 분류

Decomposition
- Seasonal-Trend Decomposition Algorithm for Long Time Series(STL)
- Robust STL
- Bootstrap STL
Statistical
- Mixture of Gaussian Trees
- LGT (Local and Global Trend)
- Mixture of AR (MAR) models (AR : AutoRegressive)
(Deep) Learning
- Embedding Space
- Deep Generative Models
- Automated Data Augmentation

2) Decomposition

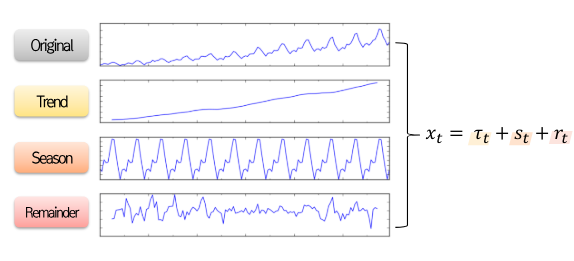
Decomposition 기법은 시계열 데이터를 Trend, Season, Remainder로 분해하는 STL 기법을 활용한 증강 기법입니다.

Seasonal-Trend Decomposition Algorithm for Long Time Series(STL)
Robust STL
- STL을 통해 Trend, Season, Remainder를 분해한 다음 가중치를 조절하여 데이터를 생성할 수 있습니다.
Bootstrap STL
- STL을 거치면서 생긴 Remainder에 BootStrap을 적용하여 데이터를 증강하는 기법으로 Bootstrapping을 적용하여 증강 데이터를 생성한 다음 Trend와 Season을 다시 추가하여 새로운 시계열 데이터를 생성합니다.

3) Statistical Generative Model

Statistical Generative model은 시계열 데이터의 conditional distribution을 반영한 데이터 증강 기법으로 t시점에서의 증강 기법을 통해 생성된 데이터는 이전 포인트의 영향을 받는다고 가정하는 것으로 시작합니다.

Mixture of Gaussian Trees
- Mixture of Gaussian trees를 활용하여 멀티모달 환경에서의 소수 클래스를 오버 샘플링하여 데이터 불균형 분류 문제를 해결하려고 함.
- 이는 TimeSeries correlations between neighboring points를 고려하여 모델링하였다는 점에서 기존 오버샘플링 기법과 차이가 있음.
LGT (Local and Global Trend)
- 통계 알고리즘으로써 계산된 해당 알고리즘으로 계산된 매개변수 및 예측 경로의 표본을 사용함.
Mixture of AR (MAR) models (AR : AutoRegressive)
- MAR 모델을 활용하여 시계열 집합을 시뮬레이션하고 시계열 Feature space에서 생성된 시계열의 다양성과 적용범위를 조사함

4) (Deep) Learning method

4.1) Embedding Space

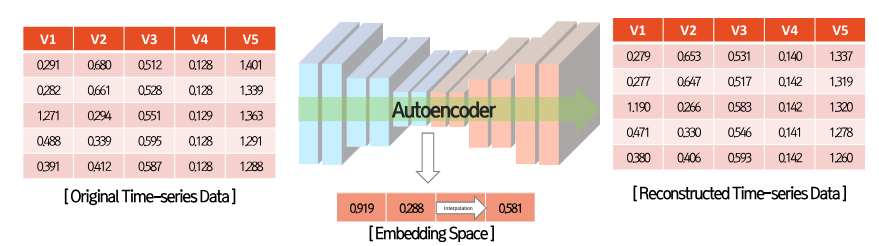
Embedding Space기법은 데이터 증강을 학습된 Embedding Space로 부터 수행할 수 있다는 연구입니다. Raw input에 대한 데이터 증강보다 embedded input에 대한 데이터 증강이 효과적임을 주장하는 방법입니다. Sequence AutoEncoder를 통해 Encoder를 학습하고, Encoder의 입력에 조금 변형된 데이터를 넣고 데이터 증강을 수행합니다.

4.2) Deep Generative Models

Generative Adversarial Network(GAN)과 RNN을 결합한 모델인 RGAN과 RCGAN을 활용하여 데이터를 증강하는 기법입니다. 이미지 생성에 주로 사용되는 Deep Generative Models(DGM)을 시계열 데이터 생성에 적용한 사례로써 Recurrent GAN(RGAN) 과 TimeGAN 두 알고리즘이 대표적입니다.

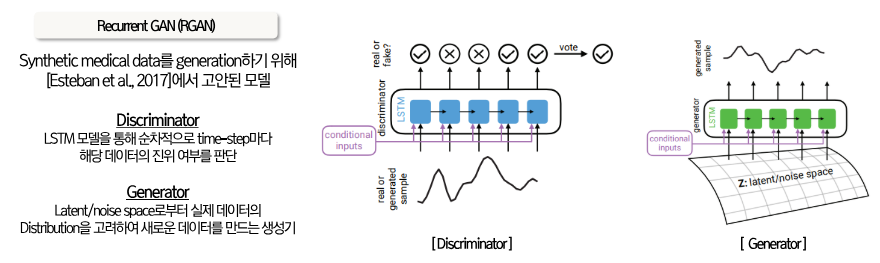
RGAN : 실제 시계열 데이터의 시퀀스와 유사한 데이터를 생성함
RCGAN : 일부 조건부 입력에 따라 실제 시계열 데이터의 시퀀스와 유사한 데이터를 생성함

4. Conclusion

시계열 데이터만을 위한 데이터 증강 기법의 필요성은 대두되고 있다. 높은 성능 향상을 가져온 이미지, 자연어, 스피치 등에 적합한 증강 기법은 시계열 데이터에 적용하기 어렵다.

기존 연구에 Basic Approches와 Advanced Approaches를 적용해볼 필요가 있다.

Reference

저작자표시 비영리 변경금지