[Metrics] 분류 모델 평가를 위한 지표는 어떻게 선정해야 하는가?
모델 평가지표를 선택할 때에는 해당 문제의 특성과 목표, 그리고 모델이 사용되는 상황을 고려해야 합니다. 다양한 모델 평가지표 중에서 어떤 것을 선택할지 결정하는 데에는 여러 요소가 영향을 미칩니다.
모델 지표 선택 시 고려사항
- 해결하려는 문제에 대한 정확한 이해가 필요
- 분류 문제인지 회귀 문제인지를 고려해야 합니다. 분류 문제에서는 정확도(Accuracy), 정밀도(Precision), 재현율(Recall), F1 스코어 등이 중요한 평가지표입니다. 회귀 문제에서는 평균 제곱 오차(Mean Squared Error), 평균 절대 오차(Mean Absolute Error) 등이 일반적입니다.
- 데이터의 불균형 문제에 대한 고민
- 클래스 간의 샘플 수가 불균형하다면 정확도만으로는 모델 성능을 올바르게 평가할 수 없습니다. 이런 경우에는 정밀도, 재현율, F1 스코어와 같은 지표를 함께 고려해야 합니다.
- 모델에서 평가하고자 하는 목적이 무엇인가
- 모델을 어떤 목적으로 사용하느냐에 따라 적절한 평가지표가 달라질 수 있습니다. 예를 들어, 이진 분류 모델에서 스팸 메일을 예측하는 경우, 재현율이 더 중요할 수 있습니다.
- 모델이 실제 적용되었을 때 최소한 보장이 되어야 하는 조건
- 어떤 메트릭들을 선정하고 비교하여 가장 좋은 모델을 선택할 것인가
- 다중 지표의 활용
- 때로는 단일 평가지표만으로 모델의 성능을 정확하게 파악하기 어려울 수 있습니다. 따라서 여러 평가지표를 종합적으로 고려하여 ganz 포괄적인 평가를 수행할 필요가 있습니다.
이러한 고려 사항을 토대로 모델 평가지표를 선택하면 더 나은 모델 평가와 의사 결정이 가능합니다.
1. 분류 모델에 대한 평가 지표
Confusion Matrix
이진 분류 모델에 대한 결과를 한눈에 표시하는 방법으로 Confusion Matrix를 활용합니다. Confusion Matrix는 분류 모델의 예측 결과를 행렬로 나타낸 것입니다. 주로 이진 분류에서 사용되며, 2x2 행렬로 참 양성(True Positive), 참 음성(True Negative), 거짓 양성(False Positive), 거짓 음성(False Negative) 등의 예측 결과를 나타냅니다.
행렬 요소
- True Positive (TP): 실제 양성인 경우를 정확하게 양성으로 예측한 경우
- True Negative (TN): 실제 음성인 경우를 정확하게 음성으로 예측한 경우
- False Positive (FP): 실제 음성인데 양성으로 잘못 예측한 경우 (Type I 오류)
- False Negative (FN): 실제 양성인데 음성으로 잘못 예측한 경우 (Type II 오류)

Accuracy (정확도)
가장 직관적으로 전체 데이터 중 정답을 맞춘 샘플들의 비율입니다. 정확도는 가장 기본적이고 직관적인 평가 지표 중 하나입니다. 예측이 올바르게 되었는지를 측정하는 데 사용됩니다.
$$ Accuracy = \frac{TP+TN}{TP+FP+FN+TN} $$
클래스 불균형에 취약: 클래스의 분포가 불균형할 때(특정 클래스의 샘플 수가 다른 클래스에 비해 월등히 많거나 적을 때) 정확도만으로 모델의 성능을 평가하기 어려울 수 있습니다. 높은 정확도를 보일 수 있지만 실제로 중요한 클래스에 대한 예측이 잘못되는 경우가 있을 수 있습니다.
아래 표를 보면 첫 번째에서 소수 클래스에 대해 예측이 0%이지만, 마지막 표는 소수 클래스 예측 100%를 나타낸다. 하지만 Acuuracy는 3개의 표 모두 0.9로 동일한 지표를 나타낸다.

이러한 특성으로 인해 모델 간 성능 비교 시 Accuracy 사용은 좋지 않습니다. Accuracy 만이 아닌 Type-1, Type-2 에러도 함께 확인해야 합니다.
데이터의 특성을 고려해야 함: 정확도를 사용할 때에는 데이터의 특성을 고려해야 합니다. 예를 들어, 클래스 간 샘플 수의 차이가 클 때에는 다른 평가 지표를 함께 고려하는 것이 더 적절할 수 있습니다.
Sensitivity (민감도) / Recall (정밀도)
민감도(Sensitivity), 또는 재현율(Recall)은 분류 모델에서 양성 클래스(Positive Class)에 속하는 샘플 중 실제로 양성 클래스로 예측된 비율을 나타내는 지표입니다. 즉 양성의 샘플을 잘 찾는데 초점을 맞춘 지표입니다. 실제 양성 중에서 얼마나 많은 샘플을 모델이 양성으로 정확하게 예측하는지를 측정합니다. 민감도가 높을 경우, 양성 결과를 놓치는 경우를 막을 수 있습니다.

$$ Sensitivity = \frac{TP}{TP + FN} $$
Specificity (특이도)
특이도(Specificity)는 음성 클래스(Negative Class)에 속하는 샘플 중 실제로 음성 클래스로 예측된 비율을 나타내는 지표입니다. 즉, 실제 음성 중에서 모델이 음성으로 정확하게 예측한 비율을 측정합니다.정상을 정상이라고 진단하는 비율로써 검사 비용이 꽤 비싼 경우 특이도가 중요해 집니다.

$$ Specificity = \frac{TN}{TN + FP} $$
- 음성 클래스의 정확도: 음성 클래스를 실제로 음성으로 정확하게 예측하는 능력을 측정합니다. 특이도는 모델이 음성 클래스를 얼마나 잘 분류하는지를 나타냅니다.
- 클래스 불균형에 강건: 클래스 간 샘플 수가 불균형한 경우, 특이도는 높은 성능 평가 지표입니다. 특히, 거짓 양성을 줄이는 것이 중요한 경우에 사용됩니다.
- 거짓 양성에 민감: 거짓 양성을 최소화하고 싶을 때 특이도를 주요 지표로 사용합니다. 예를 들어, 특정 질병이 없는데 있다고 잘못 예측하는 것을 피하려고 할 때 유용합니다.
특이도는 모델이 실제 음성을 얼마나 잘 예측하는지를 나타내는 중요한 평가 지표입니다. 특히, 실제 음성을 정확하게 예측하고 거짓 양성을 최소화하는 것이 중요한 상황에서 사용됩니다. 데이터의 특성과 비즈니스 목표에 따라 적절한 성능 지표를 선택하는 것이 중요합니다.
Precision (정확도)
Precision은 모델이 Positive로 예측한 결과 중에서 실제로 Positive인 비율을 나타냅니다. 다시 말해, 모델이 True라고 예측한 것 중에서 실제로 True인 비율을 의미합니다.

이를 수식으로 나타내면 다음과 같습니다:
$$ {Precision = \frac{True Positives}{True Positives + False Positives} }$$
여기서 True Positives는 모델이 올바르게 예측한 Positive 샘플의 수이고, False Positives는 모델이 Positive로 잘못 예측한 샘플의 수입니다. Precision은 모델이 Positive로 예측한 것 중에서 얼마나 정확하게 예측했는지를 측정하여 모델의 정확성을 평가하는 데 사용됩니다.
Precision은 모델이 Positive 클래스를 얼마나 정확하게 예측하는지를 알려주므로, 모델이 잘못된 Positive 예측을 최소화하고자 할 때 중요한 지표입니다. 그러나 Precision만으로 모델을 평가하는 것은 충분하지 않을 수 있습니다. 예를 들어, 모든 Positive 샘플을 Negative로 예측하는 모델은 Precision이 높을 수 있지만 실제로 중요한 Positive 샘플을 놓치는 문제가 발생할 수 있습니다. 따라서 Recall(재현율)과 함께 고려하는 것이 중요합니다.
Precision은 Recall과 트레이드 오프 관계에 있습니다. Precision을 높이면 False Positive를 줄이지만, 이로 인해 False Negative가 증가할 수 있습니다. 따라서 프로젝트나 문제의 특성에 맞게 Precision과 Recall 사이의 균형을 찾아야 합니다. 종종 두 지표를 조합한 F1 Score와 같은 조화 평균 지표를 사용하여 모델의 성능을 종합적으로 평가하기도 합니다.
요약하자면, Precision은 모델이 Positive로 예측한 것 중에서 얼마나 정확하게 예측했는지를 나타내며, 모델의 성능을 평가하는 데 중요한 지표 중 하나입니다.
F1 Score
F1 Score는 Precision과 Recall의 조화 평균으로, 모델의 정확성과 완전성을 모두 고려하여 평가합니다. 먼저, Precision과 Recall을 간단히 복습해보겠습니다. Precision은 모델이 Positive로 예측한 것 중에서 실제로 Positive인 비율을 나타내며, Recall은 실제로 Positive인 것 중에서 모델이 Positive로 예측한 비율을 나타냅니다.
F1 Score는 Precision과 Recall 사이의 균형을 평가하는 지표로, 다음과 같은 공식으로 계산됩니다:
$$ { F1 Score = 2 × \frac{Precision × Recall}{Precision + Recall} } $$
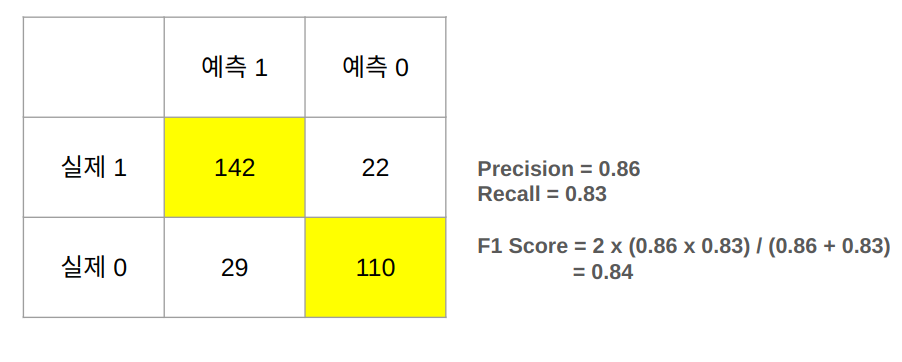
F1 Score는 Precision과 Recall이 모두 고려되기 때문에, 이 둘 사이의 균형을 나타냅니다. 모델이 얼마나 많은 True Positives를 찾고 동시에 False Positives를 줄이는지를 반영합니다.
이 메트릭은 불균형한 클래스 분포를 가진 데이터셋에서 특히 유용합니다. 예를 들어, Positive 클래스가 Negative 클래스에 비해 매우 적은 경우에는 모든 샘플을 Negative로 예측하는 모델의 Accuracy가 높더라도 실제로 중요한 Positive 샘플을 놓치는 문제가 발생할 수 있습니다. 이런 상황에서 F1 Score는 모델의 성능을 더 정확하게 평가할 수 있습니다.
F1 Score는 모델의 성능을 하나의 숫자로 요약하여 비교하기 용이하며, 특히 Precision과 Recall이 중요한 상황에서 유용합니다. 그러나 F1 Score도 모든 상황에 적합한 메트릭은 아니며, 프로젝트의 목표와 데이터의 특성을 고려하여 적합한 평가 지표를 선택하는 것이 중요합니다. 종종 Precision, Recall, 그리고 F1 Score를 함께 고려하여 모델의 성능을 종합적으로 평가하기도 합니다.
Average Strategy - Micro / Macro / Weighted
분류 모델에서 사용되는 메트릭 전략으로 Micro, Macro, Weighted 세 가지가 있습니다. 이들은 다중 클래스 분류에서 모델의 성능을 측정하는 데 사용됩니다. 각각은 서로 다른 방식으로 클래스별 지표들을 결합하여 전체적인 모델 성능을 나타냅니다.
Micro 평가
Micro 평가는 모든 클래스의 예측과 실제 값에 대해 TP, FP, FN을 모두 합친 후, Precision, Recall, F1 Score 등을 계산합니다.
모든 클래스를 동등하게 다루며, 각 샘플을 같은 비중으로 다루기 때문에 데이터의 불균형이 적은 경우에 유용합니다.
Micro 평가는 모든 클래스를 하나의 대규모 클래스로 취급하여 전체적인 성능을 측정합니다.
$$ { Micro Precision = \frac{TP + TN}{TP+FP+FN+TN} } $$
$$ { Micro Recall = \frac{TP + TN}{TP+FP+FN+TN} } $$
$$ { Micro F1 Score = \frac{Precision_{Micro} × Recall_{Micro}}{Precision_{Micro} + Recall_{Micro}} } $$
Macro 평가
Macro 평가는 각 클래스별 Precision, Recall, F1 Score 등을 개별적으로 계산한 후, 이들의 평균을 구합니다.
각 클래스마다 독립적으로 성능을 측정하여 평균을 내기 때문에, 클래스 간 불균형이 심한 경우에 유용합니다.
이 방법은 클래스마다 동일한 가중치를 부여하여 평균을 계산합니다.
$$ { Macro Precision = \frac{Precision1 + Precision2}{2} } $$
$$ { Macro Recall = \frac{Recall1 + Recall2}{2} } $$
$$ { Macro F1 Score = \frac{Precision_{Macro} × Recall_{Macro}}{Precision_{Macro} + Recall_{Macro}} } $$
Weighted 평가
Weighted 평가는 클래스별 샘플 수에 따라 가중 평균을 계산합니다.
각 클래스의 샘플 수를 고려하여 각 클래스의 Precision, Recall, F1 Score 등을 가중 평균하여 전체적인 성능을 평가합니다.
이 방법은 클래스마다 샘플 수에 따라 중요도를 부여하므로 데이터의 불균형을 고려하여 성능을 평가하는 데 유용합니다.
이러한 평가 전략은 데이터셋의 특성과 모델 평가 시 고려해야 하는 요소에 따라 선택되어야 합니다. 데이터의 클래스 분포, 각 클래스의 중요도, 그리고 모델이나 프로젝트의 목적에 따라 적절한 평가 전략을 선택하여 모델의 성능을 정확하게 평가할 수 있습니다.
